পৃষ্ঠাটি লোড হচ্ছে . . .
দয়াকরে অপেক্ষা করুন।
"লোডিং সময়" আপনার ইন্টারনেট স্পিড এর উপর নির্ভরশীল।
পৃষ্ঠাটি লোড হচ্ছে . . .
দয়াকরে অপেক্ষা করুন।
"লোডিং সময়" আপনার ইন্টারনেট স্পিড এর উপর নির্ভরশীল।
প্রশ্ন: \(\frac{1}{4}-\frac{1}{6}+\frac{1}{9}-\frac{2}{27}+\dots \) ধারাটির অসীম পদের সমষ্টি কত? ৪৩তম বিসিএস
| (ক) S∞ = 3 | (খ) S∞ = 20 |
| (গ) S∞ = \(\frac{20}{3} | (ঘ) S∞ = \(\frac{3}{20} |
উত্তর: S∞ = \(\frac{3}{20}
এখানে প্রথম পদ a=1/4
সাধারণ অন্তর r= (-1/6) /(1/4) =-2/3
S∞= a/(1-r)
=(1/4)/ {1-(-2/3)}
=(1/4) / {1+(2/3)}
=(1/4)/(5/3)
=1/4 ×3/5
=3/20
প্রশ্ন লিস্ট করে পড়তে লগইন করুন।
প্রশ্ন: একটি কোণের মান তার সম্পূরক কোণের মানের অর্ধেকের সমান। কোনটির মান কত? ৪৩তম বিসিএস
| (ক) ১২০° | (খ) ৩০° |
| (গ) ৯০° | (ঘ) ৬০° |
উত্তর: ৬০°
x° + 2x°=180° [ সম্পূরক কোণ তাই 180 ]
or, 3x°=180°
∴ x=180/3=60°
প্রশ্ন লিস্ট করে পড়তে লগইন করুন।
প্রশ্ন: ২০% যৌগিক মুনাফায় মূলধন ১০০০ টাকা ২ বছরের জন্য বিনিয়োগ করা হলো। যদি যৌগিক মুনাফা অর্ধ বছর হিসেবে ধরা হয়, তাহলে চক্রবৃদ্ধি মূলধন কত? ৪৩তম বিসিএস
| (ক) \({12^4}\) | (খ) \({11^4}\) |
| (গ) \({10^4}\) | (ঘ) \({9^4}\) |
উত্তর: \({11^4}\)
,
আমরা জানি, চক্রবৃদ্ধি মূলধন
\(C=P(1+r)^{n}\)
এখানে ,
p=10000
r= 20/2 =10% [অর্ধ বছর তাই ২ দ্বারা ভাগ ]
n=4 [ ২ বছর দেওয়া আছে যেহেতু মুনাফা অর্ধ বছর হিসেবে ধরা হয়েছে তাই দ্বিগুণ হবে ]
এখন,
\(C=1000\times \left(1+\frac{10}{100}\right)^{4}\)
\(C=1000\times (1.1)^{4}\)
= \({11^4}\)
প্রশ্ন লিস্ট করে পড়তে লগইন করুন।
প্রশ্ন: x= √4 +√3 হলে \(x^{3}+\frac{1}{x^{3}}\) এর মান কত? ৪৩তম বিসিএস
| (ক) 5√3 | (খ) 2√5 |
| (গ) 5√2 | (ঘ) 52 |
উত্তর: 52
Shortcut Formula:
যদি \(x=\sqrt{a}+\sqrt{b}\) হয় এবং \(a\) ও \(b\) এর পার্থক্য ১ হয় (যেমন: ৪ ও ৩ এর পার্থক্য ১),তবে:
১. \(x+\frac{1}{x}=2\times \text{\ }\)
২. \(x^{3}+\frac{1}{x^{3}}=p^{3}-3p\) (যেখানে \(p=x+\frac{1}{x}\))
এই অংকের ক্ষেত্রে প্রয়োগ:
ধাপ ১: \(x=\sqrt{4}+\sqrt{3}\)।
বড় সংখ্যাটি হলো \(\sqrt{4}=2\)।
সুতরাং, \(x+\frac{1}{x}=2\times 2=\mathbf{4}\)
ধাপ ২:
এখন \(p=4\) ধরে সরাসরি সূত্রে বসিয়ে দিন:\(x^{3}+\frac{1}{x^{3}}=4^{3}-(3\times 4)\)\(=64-12=\mathbf{52}\)
মনে রাখার টিপস: বর্গমূলের পার্থক্য ১ হলে: \(x=\sqrt{4}+\sqrt{3}\) হলে \(1/x\)
হবে সরাসরি \(\sqrt{4}-\sqrt{3}\)।\(x^{2}+\frac{1}{x^{2}}\)
চাইলে: সরাসরি \(p^{2}-2\) বা \(4^{2}-2=14\)।
পার্থক্য ১ না হলে: তখন \(1/x\) বের করে যোগ করতে হবে।
প্রশ্ন লিস্ট করে পড়তে লগইন করুন।
প্রশ্ন: একটি নৌকা পানির লেভেলে বাঁধা দড়ি দ্বারা একটি ডকের দিকে টানা হয়। নৌকাটি যখন ডক থেকে ১২ ফুট দূরে থাকে, তখন নৌকা থেকে ডক পর্যন্ত দড়ির দৈর্ঘ্য পানির উপর ডকের উচ্চতার দ্বিগুণের চেয়ে ৩ ফুট লম্বা হয়। তাহলে ডকের উচ্চতা কত? ৪৩তম বিসিএস
| (ক) ৮ ফুট | (খ) ৪ ফুট |
| (গ) ৫ ফুট | (ঘ) ৯ ফুট |
উত্তর: ৫ ফুট
➡️ ধাপ ১: সমীকরণ গঠন ধরি,
ডকের উচ্চতা \(h\) ফুট।
প্রশ্নানুসারে, দড়ির দৈর্ঘ্য হবে উচ্চতার দ্বিগুণের চেয়ে ৩ ফুট বেশি,
অর্থাৎ \((2h+3)\) ফুট।
নৌকাটি ডক থেকে ১২ ফুট দূরে অবস্থিত। যেহেতু ডক, দড়ি এবং পানির দূরত্ব একটি সমকোণী ত্রিভুজ গঠন করে,
তাই পিথাগোরাসের সূত্রানুযায়ী:
\(h^{2}+12^{2}=(2h+3)^{2}\)
➡️ ধাপ ২: সমীকরণ সরলীকরণ সমীকরণটি সমাধান করি
:\(h^{2}+144=4h^{2}+12h+9\)
সবগুলো পদ একপাশে আনলে পাই:
\(3h^{2}+12h-135=0\)উভয় পক্ষকে ৩ দ্বারা ভাগ করলে:
\(h^{2}+4h-45=0\)
➡️ ধাপ ৩: উৎপাদকে বিশ্লেষণ মিডল টার্ম ব্রেকিং পদ্ধতি ব্যবহার করে:\(h^{2}+9h-5h-45=0\)\((h+9)(h-5)=0\)যেহেতু উচ্চতা ঋণাত্মক হতে পারে না,
তাই \(h+9=0\) গ্রহণযোগ্য নয়।
সুতরাং, \(h-5=0\) বা \(h=5\)।
প্রশ্ন লিস্ট করে পড়তে লগইন করুন।
প্রশ্ন: O কেন্দ্রবিশিষ্ট বৃত্তের x কোণের মান কত? ৪৩তম বিসিএস
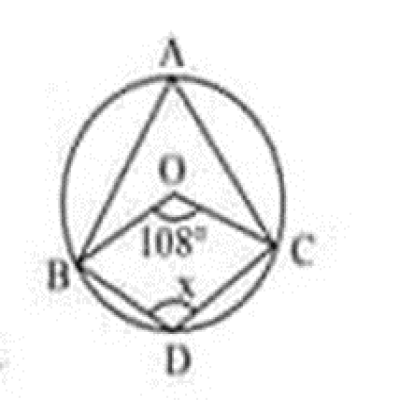
| (ক) 108 | (খ) 54° |
| (গ) 126° | (ঘ) 72° |
উত্তর: 126°
প্রশ্ন লিস্ট করে পড়তে লগইন করুন।
প্রশ্ন: একটি অনুষ্ঠানে কিছু লোক উপস্থিত ছিল। তারা কেবল একজন মাত্র একজনের সাথে একবার করমর্দন করতে পারবে। যদি করমর্দনের সংখ্যা ৩০০ হয়, তাহলে ঐ অনুষ্ঠানে কতজন লোক উপস্থিত ছিল? ৪৩তম বিসিএস
| (ক) 30 | (খ) 60 |
| (গ) 24 | (ঘ) 25 |
উত্তর: 25
\({}^{n}C_{2}\)।= 300
n(n-1)/2= 300
n(n-1)= 600
25(25-1)= 600
So,
n= 25
প্রশ্ন লিস্ট করে পড়তে লগইন করুন।