পৃষ্ঠাটি লোড হচ্ছে . . .
দয়াকরে অপেক্ষা করুন।
"লোডিং সময়" আপনার ইন্টারনেট স্পিড এর উপর নির্ভরশীল।
পৃষ্ঠাটি লোড হচ্ছে . . .
দয়াকরে অপেক্ষা করুন।
"লোডিং সময়" আপনার ইন্টারনেট স্পিড এর উপর নির্ভরশীল।
প্রশ্ন: প্রশ্ন ৪০ তম বিসিএস
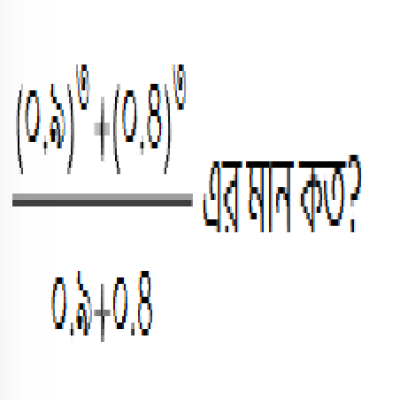
| (ক) ০.৮১ | (খ) ০.৫১ |
| (গ) ০.৬১ | (ঘ) ০.৩৬ |
উত্তর: ০.৬১
প্রশ্ন লিস্ট করে পড়তে লগইন করুন।
প্রশ্ন: 3x – 2 > 2x-1 এর সমাধান সেট কোনটি? ৪০ তম বিসিএস
| (ক) ( 1,∞ ) | (খ) [1/2, ∞ ) |
| (গ) [ 1,∞ ) | (ঘ) [-1,∞ ) |
উত্তর: [ 1,∞ )
3x - 2 > 2x - 1
=> 3x - 2x > 2 - 1
=> x > 1
নির্ণেয় সমাধান সেটঃ (1,∞)
প্রশ্ন লিস্ট করে পড়তে লগইন করুন।
প্রশ্ন: \(6x^{2}-7x-4=0\) সমীকরণে মূলদ্বয়ের প্রকৃতি কোনটি? ৪০ তম বিসিএস
| (ক) অবাস্তব | (খ) বাস্তব ও অসমান |
| (গ) পূর্ণ বর্গ সংখ্যা | (ঘ) বাস্তব ও সমান |
উত্তর: বাস্তব ও অসমান
\(6x^{2}-7x-4=0\) সমীকরণের মূলদ্বয় বাস্তব, অসমান ও অমূলদ। ধাপ ১: সমীকরণের সহগ নির্ণয় প্রদত্ত দ্বিঘাত সমীকরণটি হলো \(6x^{2}-7x-4=0\)।একে আদর্শ দ্বিঘাত সমীকরণ \(ax^{2}+bx+c=0\) এর সাথে তুলনা করলে পাই:\(a=6\)\(b=-7\)\(c=-4\) ধাপ ২: নিশ্চয়ক (Discriminant) নির্ণয় কোনো দ্বিঘাত সমীকরণের মূলের প্রকৃতি এর নিশ্চয়ক \(D\) এর ওপর নির্ভর করে, যেখানে \(D=b^{2}-4ac\)।\(D=(-7)^{2}-4(6)(-4)\)\(D=49+96\)\(D=145\)ধাপ ৩: মূলের প্রকৃতি নির্ধারণ নিশ্চয়ক \(D\) এর মান থেকে আমরা দেখতে পাই:১. যেহেতু \(D>0\) (অর্থাৎ \(145>0\)), তাই মূলদ্বয় বাস্তব ও অসমান।২. যেহেতু \(145\) কোনো পূর্ণবর্গ সংখ্যা নয়, তাই মূলদ্বয় অমূলদ।
প্রশ্ন লিস্ট করে পড়তে লগইন করুন।
প্রশ্ন: যদি \(x^{4}-x^{2}+1=0\) হয়, তবে \(x^{3}+\frac{1}{x^{3}}=\) ? ৪০ তম বিসিএস
| (ক) 2 | (খ) 1 |
| (গ) 3 | (ঘ) 0 |
উত্তর: 0
এই সমস্যাটি দ্রুত সমাধানের জন্য নিচের শর্টকাট টেকনিকটি অনুসরণ করতে পারেন: ১. প্রথম ধাপ (\(x^{2}+1/x^{2}\) বের করা):\(x^{4}-x^{2}+1=0\) সমীকরণ থেকে সরাসরি লেখা যায় \(x^{2}+\frac{1}{x^{2}}=1\) (মাঝের পদের সহগ ১ হলে যোগফল ১ হয়)। ২. দ্বিতীয় ধাপ (\(x+1/x\) বের করা):আমরা জানি, \((x+\frac{1}{x})^{2}=(x^{2}+\frac{1}{x^{2}})+2=1+2=3\)সুতরাং, \(x+\frac{1}{x}=\sqrt{3}\) ৩. তৃতীয় ধাপ (সরাসরি সূত্র):যদি \(x+\frac{1}{x}=a\) হয়, তবে \(x^{3}+\frac{1}{x^{3}}=a^{3}-3a\)।এখানে \(a=\sqrt{3}\) বসিয়ে পাই:\((\sqrt{3})^{3}-3(\sqrt{3})=3\sqrt{3}-3\sqrt{3}=\mathbf{0}\) মনে রাখার টিপস:পরীক্ষায় যদি দেখেন \(x^{2}+\frac{1}{x^{2}}=1\) অথবা \(x+\frac{1}{x}=\sqrt{3}\) এসেছে, তবে \(x^{3}+\frac{1}{x^{3}}\) এর মান সব সময় ০ হবে।
প্রশ্ন লিস্ট করে পড়তে লগইন করুন।
প্রশ্ন: \((x^{x})^{\sqrt{x}}\) = \((x\sqrt{x})^{x}\) হলে, x এর মান কত? ৪০ তম বিসিএস
| (ক) \(\frac{5}{4}\) | (খ) \(\frac{2}{3}\) |
| (গ) \(\frac{9}{4}\) | (ঘ) \(\frac{3}{2}\) |
উত্তর: \(\frac{9}{4}\)
এই সমস্যাটি দ্রুত সমাধানের জন্য নিচের শর্টকাট টেকনিকটি অনুসরণ করুন: ১. পাওয়ারগুলো সরল করা:আমরা জানি, \(x\sqrt{x}=x^{1.5}\) এবং \(\sqrt{x}=x^{0.5}\)।সমীকরণটি দাঁড়ায়: \((x^{x})^{x^{0.5}}=(x^{1.5})^{x}\) ২. পাওয়ারের সাথে পাওয়ার গুণ করা:বামে পাওয়ার হবে: \(x\times x^{0.5}=x^{1.5}\)ডানে পাওয়ার হবে: \(1.5\times x=1.5x\) ৩. পাওয়ার দুটির তুলনা:যেহেতু ভিত্তি \(x\) উভয় দিকে সমান, তাই পাওয়ার দুটিও সমান হবে:\(x^{1.5}=1.5x\) ৪. সরাসরি উত্তর বের করা:উভয় পক্ষকে \(x\) দিয়ে ভাগ করলে থাকে:\(x^{0.5}=1.5\) (এখানে \(x^{0.5}\) মানে \(\sqrt{x}\))বা, \(\sqrt{x}=\frac{3}{2}\) এখন বর্গ করলে:\(x=\frac{9}{4}\) (বা ২.২৫) টিপস: অপশনে যদি ১ থাকে, তবে সেটিও সঠিক উত্তর হতে পারে কারণ ১-এর সকল পাওয়ার সমান। তবে গাণিতিক সমাধানে ৯/৪-ই প্রধান উত্তর।
প্রশ্ন লিস্ট করে পড়তে লগইন করুন।
প্রশ্ন: \(\log _{a}1=0\) ? ৪০ তম বিসিএস
| (ক) a≠0,a>1 | (খ) a≠1,a<0 |
| (গ) a> 0,a≠1 | (ঘ) a>0,a=1 |
উত্তর: a> 0,a≠1
\(\log _{a}1=0\) হওয়ার জন্য শর্তটি হলো: \(a>0\) এবং \(a\ne 1\)। ব্যাখ্যা:লগারিদমের সংজ্ঞা অনুযায়ী, ভিত্তিকে (\(a\)) অবশ্যই ধনাত্মক হতে হয় এবং তা ১ এর সমান হতে পারবে না। কারণ:১. ভিত্তি ঋণাত্মক হলে লগারিদম সংজ্ঞায়িত হয় না।২. ভিত্তি ১ হলে তার ওপর যেকোনো পাওয়ার বসালে ফলাফল সবসময় ১-ই থাকে, যা থেকে নির্দিষ্ট মান পাওয়া সম্ভব নয়।
প্রশ্ন লিস্ট করে পড়তে লগইন করুন।
প্রশ্ন: প্রশ্ন ৪০ তম বিসিএস
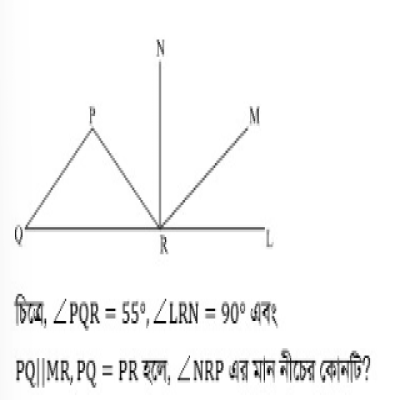
| (ক) 90° | (খ) 45° |
| (গ) 90° | (ঘ) 35° |
উত্তর: 35°
প্রশ্ন লিস্ট করে পড়তে লগইন করুন।
প্রশ্ন: P = {x : x, 12 এর গুণনীয়কসমূহ} এবং Q = {x : x, 3 এর গুণিতক এবং x≤12} হলে, P – Q কত? ৪০ তম বিসিএস
| (ক) {1,2,4} | (খ) {1,,3,4} |
| (গ) {1,2,6} | (ঘ) {1,3,6} |
উত্তর: {1,2,4}
P - Q = { 1, 2, 3, 4, 6, 12 } - { 3, 6, 9, 12 }
= { 1, 2, 4 }
নির্ণয় সেট { 1, 2, 4 }
প্রশ্ন লিস্ট করে পড়তে লগইন করুন।
প্রশ্ন: \(\cos \left(\frac{n\pi }{2}\right)\) অনুক্রমটির চতুর্থ পদ কোনটি? ৪০ তম বিসিএস
| (ক) 1 | (খ) 2 |
| (গ) 0 | (ঘ) -1 |
উত্তর: 1
\(\cos \left(\frac{n\pi }{2}\right)\) অনুক্রমটির চতুর্থ পদ হলো ১।
হিসাব:
চতুর্থ পদ বের করার জন্য অনুক্রমটিতে \(n=4\) বসাতে হবে।
অতএব, ৪র্থ পদ = \(\cos \left(\frac{4\pi }{2}\right)\)
= \(\cos (2\pi )\)
= ১।
প্রশ্ন লিস্ট করে পড়তে লগইন করুন।
প্রশ্ন: ৬ জন খেলোয়াড়কে সমান সংখ্যক দুইটি দলে কত ভাবে বিভক্ত করা যায়? ৪০ তম বিসিএস
| (ক) 20 | (খ) 10 |
| (গ) 30 | (ঘ) 60 |
উত্তর: 10
৬ জন খেলোয়াড়কে সমান সংখ্যক (৩ জন করে) দুইটি দলে মোট ১০ ভাবে বিভক্ত করা যায়। ৬ জন থেকে ৩ জন নিয়ে প্রথম দল গঠন করা যায় \({}^{6}C_{3}=20\) উপায়ে, কিন্তু দলগুলো সমান হওয়ায় এবং দলগুলোর মধ্যে কোনো নাম বা ক্রম না থাকায়, বিন্যাসটি \(2!\) বা ২ দিয়ে ভাগ করতে হয়। তাই, মোট উপায় = \(\frac{{}^{6}C_{3}}{2}=\frac{20}{2}=10\)
প্রশ্ন লিস্ট করে পড়তে লগইন করুন।
প্রশ্ন: ∆ABC এর ∠A=40° এবং ∠B=80°। ∠C এর সমদ্বিখণ্ডক AB বাহুকে D বিন্দুতে ছেদ করলে ∠CDA=? ৪১ তম বিসিএস
| (ক) ৮০° | (খ) ১১০° |
| (গ) ১০০° | (ঘ) ৯০° |
উত্তর: ১১০°
Given, A=40,B=80
We know, 180=A+B+C, C=180-40-80=60
again, a=40, c=60/2=30
180=a+c+d
d=180-40-30=110
CDA=110
প্রশ্ন লিস্ট করে পড়তে লগইন করুন।
প্রশ্ন: ৫ জন পুরুষ ও ৪ জন মহিলার একটি দল থেকে একজন পুরুষ ও দুইজন মহিলা নিয়ে কত প্রকারে একটি কমিটি গঠন করা যাবে? ৪১ তম বিসিএস
| (ক) 20 | (খ) 10 |
| (গ) 30 | (ঘ) 40 |
উত্তর: 30
৫ জন পুরুষ ও ৪ জন মহিলার একটি দল থেকে একজন পুরুষ ও দুইজন মহিলা নিয়ে মোট ৩০ প্রকারে একটি কমিটি গঠন করা যাবে।
ধাপ ১: পুরুষ সদস্য বাছাই পদ্ধতি
৫ জন পুরুষ থেকে ১ জন পুরুষ বাছাই করার উপায় সংখ্যা সমবায় বা Combination এর সূত্রানুসারে:
\({}^{5}C_{1}=\frac{5!}{1!(5-1)!}=5\)
ধাপ ২: মহিলা সদস্য বাছাই পদ্ধতি ৪ জন মহিলা থেকে ২ জন মহিলা বাছাই করার উপায়
সংখ্যা:\({}^{4}C_{2}=\frac{4!}{2!(4-2)!}=\frac{4\times 3}{2\times 1}=6\)
ধাপ ৩: কমিটির মোট সংখ্যা নির্ধারণ গণনার গুণন নীতি অনুযায়ী,
১ জন পুরুষ এবং ২ জন মহিলা নিয়ে কমিটি গঠন করার মোট উপায় সংখ্যা:\(5\times 6=30\)
প্রশ্ন লিস্ট করে পড়তে লগইন করুন।
প্রশ্ন: \(x=2^{1/3}+2^{2/3}\) হলে, \(x^{3}+6\) এর মান কত? ৪১ তম বিসিএস
| (ক) 4 | (খ) 6x |
| (গ) 4x | (ঘ) 6 |
উত্তর: 6x
\(x+2^{1/3}+2^{2/3}=0\) \(\text{,\ }x=-(2^{1/3}+2^{2/3})\)\(\text{,\ }x^{3}=-\{(2^{1/3}+2^{2/3})^{3}\}\)\(\text{,\ }x^{3}=-\{(2^{1/3})^{3}+(2^{2/3})^{3}+3\cdot 2^{1/3}\cdot 2^{2/3}(2^{1/3}+2^{2/3})\}\)\(\text{,\ }x^{3}=-\{2+4+3\cdot 2(-x)\}\)\(\text{,\ }x^{3}=-(6-6x)\)\(\text{,\ }x^{3}=-6+6x\)\(\text{,\ }\mathbf{x}^{\mathbf{3}}\mathbf{+6=6x}\)
প্রশ্ন লিস্ট করে পড়তে লগইন করুন।
প্রশ্ন: \(5^x+8.5^x+16.5^x=1\) হলে, xএর মান কত? ৪১ তম বিসিএস
| (ক) -2 | (খ) -1 |
| (গ) -3 | (ঘ) -1/2 |
উত্তর: -2
\(5^{x}=a\) \(a+8a+16a=1\)\(\text{,\ }25a=1\)\(\text{,\ }a=\frac{1}{25}\)\(\text{,\ }5^{x}=\frac{1}{5^{2}}\)\(\text{,\ }5^{x}=5^{-2}\)\(\therefore \mathbf{x=-2}\)
প্রশ্ন লিস্ট করে পড়তে লগইন করুন।
প্রশ্ন: ০.১২ + ০.০০১২ + ০.০০০০ ১২ + ……. ধারাটির অসীম পদ পর্যন্ত যোগফল- ৪১ তম বিসিএস
| (ক) \(\frac{\mathbf{112}}{\mathbf{99}}\) | (খ) \(\frac{\mathbf{4}}{\mathbf{33}}\) |
| (গ) \(\frac{\mathbf{14}}{\mathbf{99}}\) | (ঘ) \(\frac{\mathbf{4}}{\mathbf{99}}\) |
উত্তর: \(\frac{\mathbf{4}}{\mathbf{33}}\)
এখানে, a = ০.১২, r = (০.০০১২/০.১২)=০.০১
S অসীম হলে,
∴ S∞ = a /(১-r)
= ০.১২/(১-০.০১)
= ০.১২/০.৯৯
= ১২/৯৯
= ৪/৩৩
প্রশ্ন লিস্ট করে পড়তে লগইন করুন।